Toda função estabelecida pela lei de formação f(x) = ax² + bx + c, com a, b e c números reais e a ≠ 0, é denominada função do 2º grau. Generalizando temos:
F:R -> R tal que f(x) = ax2 + bx + c, com a R*, b R, c R
A representação geométrica de uma função do 2º grau é dada por uma parábola, que de acordo com o sinal do coeficiente a pode ter concavidade voltada para cima ou para baixo.
As raízes de uma função do 2º grau são os pontos onde a parábola intercepta o eixo x. Dada a função
f(x) = ax² + bx + c, se f(x) = 0, obtemos uma equação do 2º grau, ax² + bx + c = 0, dependendo do valor do discriminante Δ, podemos ter as seguintes situações gráficas:
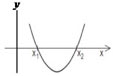
Δ > 0, a equação possui duas raízes reais e diferentes. A parábola intercepta o eixo x em dois pontos distintos.
Δ= 0, a equação possui apenas uma raiz real. A parábola intercepta o eixo x em um único ponto.

Δ < 0, a equação não possui raízes reais. A parábola não intercepta o eixo x.