Toda relação de dependência, em que uma incógnita depende do valor da outra, é denominada função. A função exponencial também possui essa mesma relação de dependência, com a diferença de que sua parte variável, representada por x, se encontra no expoente. Como nos exemplos seguintes:
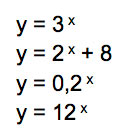
A lei de formação de uma função exponencial indica que a base elevada ao expoente x precisa ser maior que zero e diferente de um, conforme a seguinte notação:
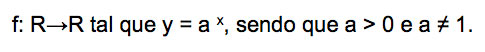
As funções exponenciais são usadas para representar situações em que a taxa de variação é considerada grande, por exemplo, em rendimentos financeiros capitalizados por juros compostos, no decaimento radioativo de substâncias químicas, desenvolvimento de bactérias e micro-organismos, crescimento populacional entre outras situações.
As funções exponenciais devem ser resolvidas utilizando, se necessário, as regras envolvendo potenciação.














