1. Quantidade de Movimento
Sempre que houver uma interação entre dois corpos, sendo que, ao menos um deles esteja em movimento, ou adquira movimento, a determinação da quantidade de movimento e do impulso é importante para o estudo dessa interação.
A quantidade de movimento é uma grandeza vetorial determinada pela massa do corpo multiplicada pelo seu vetor velocidade:

Como a massa é uma grandeza escalar, o vetor quantidade de movimento será paralelo ao vetor velocidade, tendo a mesma direção e sentido.
2. Impulso
O impulso é uma grandeza física que estuda a interação de uma força aplicada a um corpo com o tempo de aplicação. A aplicação do impulso determina a variação da quantidade de movimento (Teorema do Impulso).
Para uma força de módulo constante agindo em um intervalo de tempo o impulso é:

Como a variação do tempo é uma grandeza escalar, o vetor impulso terá sempre a mesma direção e sentido do vetor força que o ocasiona.
3. Teorema do Impulso
O impulso mede a variação da quantidade de movimento de um corpo, e pode ser deduzido:

Como anteriormente formulado, o impulso é igual a variação da quantidade de movimento.
Como exemplo, podemos citar uma situação bastante comum: um projétil que sai de um armamento provocando um recuo da arma.
No caso de um sistema em que as forças externas são nulas ou a resultante delas é nula, o impulso do sistema é nulo:
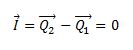
4. Choque (Colisão)
A aplicação imediata dos conceitos de quantidade de movimento e impulso, e do teorema do impulso é no estudo do choque entre corpos. Em qualquer choque entre dois ou mais corpos, se considerarmos o sistema composto apenas por eles ‒ portanto, sem a existência de forças externa ao sistema ‒ haverá sempre a conservação da quantidade de movimento.
No entanto, diferentes situações podem ocorrer:
Quando, por exemplo, dois corpos se chocam e continuam o movimento unidos, verifica-se o chamado choque perfeitamente inelástico. Neste caso, embora a quantidade de movimento se conserve, existe uma significativa perda de energia cinética do sistema.
Se, por outro lado, o choque ocorre sem deformações permanentes, pode ser classificado como choque perfeitamente elástico. Neste caso existe a conservação da quantidade de movimento bem como da energia cinética do sistema.
Existem ainda os choques parcialmente elásticos, que abrangem toda a gama de possibilidades entre os extremos do choque elástico e do inelástico.
4.1. Coeficiente de Restituição
Para o estudo dos choques definimos o conceito de coeficiente de restituição.

O numerador representa a velocidade de afastamento entre os corpos (ou seja, a velocidade com que se afastam um em relação ao outro). O denominador representa a velocidade de aproximação relativa entre eles.
No choque perfeitamente elástico, não havendo deformações permanentes, a velocidade de afastamento será igual à de aproximação e, portanto, o coeficiente de restituição será e = 1.
No choque perfeitamente inelástico, os corpos permanecem unidos, portanto não se afastam um do outro. A velocidade de afastamento é zero e, portanto, o coeficiente de restituição será e = 0.
Nos choques parcialmente elásticos a velocidade de afastamento será sempre menor que a de aproximação. Portanto, de maneira geral, teremos um valor do coeficiente de restituição compreendido entre zero e um, ou 0 < e < 1.
| Exercícios |
| 1. (Fuvest-SP) Considere as seguintes afirmações acerca de uma colisão inelástica de um sistema constituído por dois corpos. I. Existe conservação de energia cinética imediatamente antes e imediatamente após a colisão. II. Existe conservação da quantidade de movimento imediatamente antes e imediatamente após a colisão. III. Conserva-se a velocidade relativa dos corpos, antes e após a colisão. Destas afirmações: a) apenas I é correta. |
| 2. (Fuvest-SP) Um carro de massa 800 kg, em repouso, é abalroado por trás por um outro de 1 200 kg que se movimenta com velocidade 72 km/h. Supondo que a colisão tenha sido totalmente inelástica, determinar: a) a velocidade do conjunto constituído pelos dois carros imediatamente após a colisão (em km/h). b) a variação de energia cinética do sistema. |
| 3. (Unicamp-SP) Um objeto de massa m1=4,0 kg e velocidade v1=3,0 m/s choca-se com um objeto em repouso, de massa m2=2,0 kg. A colisão ocorre de forma que a perda de energia cinética é máxima, mas consistente com o princípio da conservação da quantidade de movimento. a) Quais as velocidades dos objetos imediatamente após a colisão? b) Qual a variação da energia cinética do sistema? |
Respostas:
1. b
2. a) 12 m/s
b) 96000 J
3. a) 2 m/s
b) 6 J














