Um dos truques mais úteis da matemática, a regra de 3 é um cálculo de proporcionalidade, pois envolve a resolução de duas ou mais grandezas, sempre em termos proporcionais.
Essa regrinha pode ser usada não apenas no universo matemático, mas também em outras áreas da ciência, como a Química, a Física, a Biologia – e até no nosso cotidiano.
Mas vamos à explicação. Existem dois tipos de grandezas proporcionais que aparecem nas regras de 3: as diretamente proporcionais e as inversamente proporcionais.
Como fazer regra de 3
1. Grandeza diretamente proporcional
Uma grandeza é diretamente proporcional a outra quando o aumento de uma delas implica no aumento da outra, na mesma proporção.
Um exemplo: O peso total de borrachas é diretamente proporcional ao número de borrachas que serão levadas pelo comprador, pois quanto mais unidades de borracha o comprador levar, maior será o peso total.
Dessa forma, ao dobrar o valor de uma grandeza, o valor da grandeza correspondente também será dobrado. Ou seja, mais borrachas = mais peso.
2. Grandeza inversamente proporcional
Uma grandeza é inversamente proporcional a outra quando o aumento de uma delas implica na diminuição da outra.
Exemplo: a velocidade de um carro de Fórmula 1 é inversamente proporcional ao tempo que ele demora para dar uma volta na pista, pois quanto mais rápido o carro estiver, menor será o tempo que ele irá demorar para completar todo o percurso.
3. Regra de 3 simples e regra de 3 composta
O cálculo da regra de três simples é utilizado quando pretende-se descobrir a proporção entre duas grandezas, sejam elas direta ou inversamente proporcionais.
Quando as grandezas são diretamente proporcionais, basta calcular diretamente os elementos. Por exemplo:
Um carro percorreu, em duas horas, 90 quilômetros. Mantendo a mesma velocidade, quantos quilômetros o carro irá percorrer em três horas?
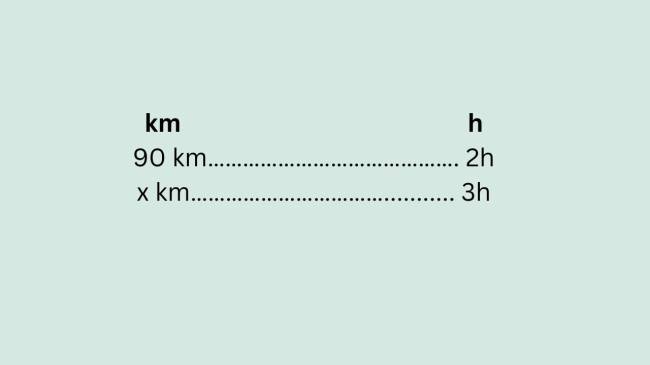
Para o cálculo, basta multiplicar os valores cruzados:
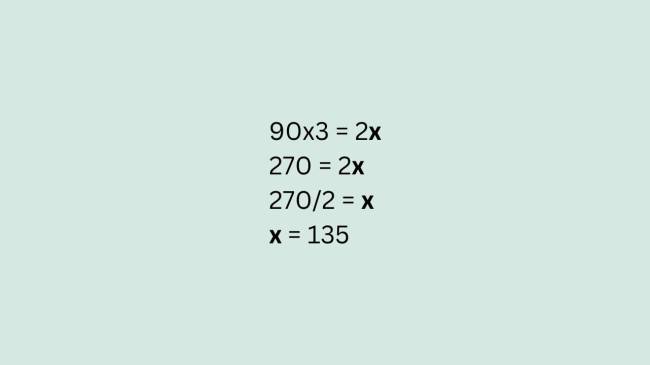
Portanto, o carro irá percorrer 135 quilômetros em três horas.
Já quando as grandezas forem inversamente proporcionais, o caminho será um pouco diferente. Vejamos:
Um carro percorre um trajeto de 200 quilômetros em quatro horas, a uma velocidade constante de 60 km/h. Em quanto tempo o mesmo carro irá percorrer esse mesmo trajeto se aumentarmos sua velocidade para 80 km/h?
Neste caso, como as grandezas de velocidade e tempo são inversamente proporcionais (quanto mais rápido o carro, menor o tempo de percurso), precisamos torná-las proporcionais. Por isso, ao invés do cálculo ser feito da forma tradicional, precisamos primeiro torná-las diretamente proporcionais.
Portanto, o cálculo deve ser feito desta maneira.

Pronto, agora que as tornamos diretamente proporcionais, basta cruzar os valores e multiplicá-los:
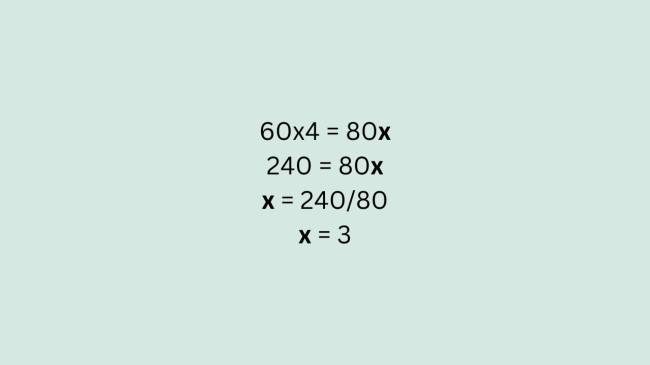
Portanto, o carro completará o trajeto em três horas.
Regra de três composta
A regra de três composta é utilizada para descobrir o valor de três ou mais grandezas. Para isso, deve-se construir uma coluna com os valores das grandezas listadas.
Exemplo: Um vestibulando que se prepara para o Enem decidiu estudar 9 horas por dia todas as 10 matérias, durante 60 dias até a data do exame. No entanto, o estudante procrastinou um pouco, e possui agora apenas 45 dias para cumprir sua meta de estudos. Quantas horas o estudante deve se dedicar às matérias por dia?
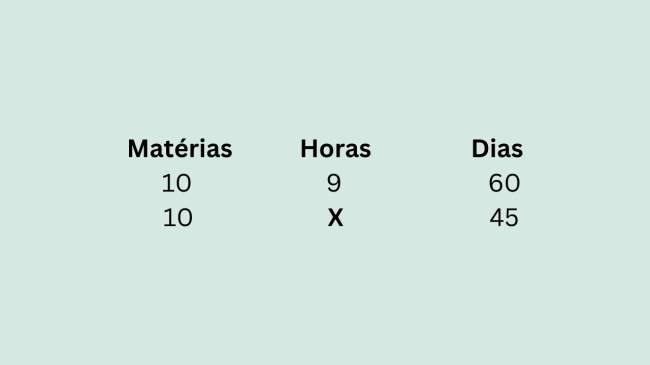
Como o número de dias é inversamente proporcional ao número de horas, precisamos realizar o mesmo caminho de cálculo da regra de três simples para grandezas inversamente proporcionais. Por isso, vamos inverter os valores dos dias, para tornar as grandezas diretamente proporcionais.
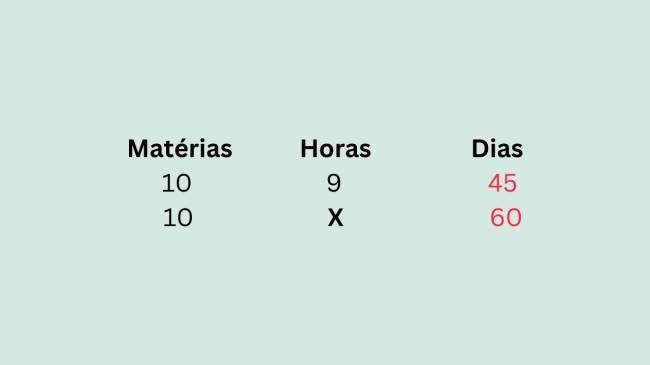
Agora, colocamos os valores em uma equação de frações. Ficará desta maneira:

Como os dois valores em cada um dos lados da equação são frações, podemos aplicar o método da regra de três simples e multiplicar os valores cruzados:
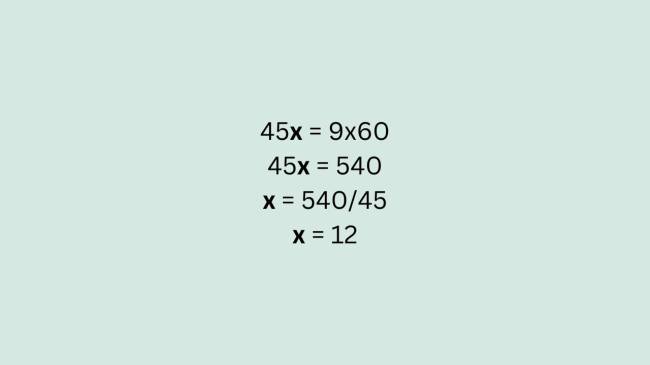
Portanto, o estudante terá que estudar 12 horas durante os 45 dias até o Enem.














