Como resolver a fórmula de Bháskara, que pegou Rayssa Leal de surpresa?
A formula de Bháskara é a maneira mais fácil de resolver uma equação de segundo grau. Entenda aqui como aplicá-la e chegar às respostas corretas
Todo estudante já se deparou com a famosa fórmula de Bháskara. Rayssa Leal, a jovem skatista brasileira que é destaque nas Olimpíadas de Paris 2024, não é exceção. A “Fadinha” foi pega de surpresa em uma entrevista, quando um repórter lhe perguntou qual era a conta. A verdade é que essa fórmula matemática nada mais é do que uma maneira mais ágil de resolver uma equação de segundo grau. Ou seja, é uma forma de se descobrir o valor de x em uma equação de segundo grau. Para isso, ela usa como base os coeficientes de x.
E aí, Fadinha, qual a resposta? 🤣😅
Você acompanha o Ça Va Paris, todos os dias no sportv2, a partir das 19h! tv📺#ÇaVaParis pic.twitter.com/gmOo7XTIBJ
— sportv (@sportv) July 29, 2024
Como resolver a fórmula de Bháskara
Para entender melhor, peguemos um modelo padrão de equação de segundo grau:
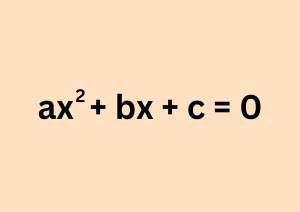
Os coeficientes, aqui neste caso, são os números reais demarcados como a, b e c. A incógnita é o x.
Veja a seguir a fórmula de Bháskara, ainda com os coeficientes genéricos, para entender como ela deve ser aplicada.
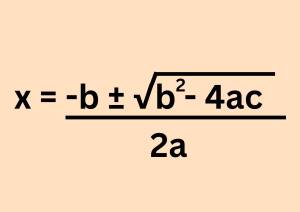
+ Enem 2023: principais fórmulas de Matemática para revisar antes da prova
Para resolver o Bháskara, basta colocar os os números a, b e c dentro da fórmula. Veja aqui um exemplo com números reais, a partir da seguinte equação:
Neste exemplo, a = 1, b = 2 e c = -3. Aqui, com os coeficientes aplicadas na fórmula de Bháskara:
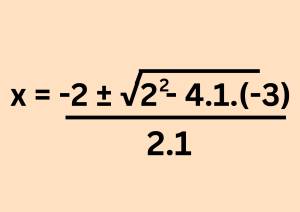
A primeira coisa a ser resolvida é o discriminante – ou seja, a conta que está abaixo da raiz quadrada. Neste caso, é a expressão: b2 – 4ac. O discriminante também é chamado de delta e representado por um triângulo (a letra grega Δ). Ou seja, se alguém quiser saber qual é o delta do Bháskara, lembre-se que é Δ = b2 – 4ac.
+ O que mais cai na prova de Matemática do Enem?
Mas voltemos à equação acima. Veja como ficaria o delta resolvido da nossa equação-exemplo:
Assim, basta tirar a raiz quadrada de 16 para chegar às respostas finais. (Lembrando que o símbolo ± quer dizer que há duas respostas para o x: é preciso fazer uma soma e uma subtração da raiz.)
Então vamos lá: a raiz quadrada de 16 é 4. Esse quatro vai ser somado e subtraído do -2. Veja abaixo:
Eis aí o resultado na nossa equação x2 + 2x – 3 = 0.
x = 1 e x = -3.
A partir de agora, para resolver uma equação de segundo grau, basta seguir a mesma lógica.
Prepare-se para o Enem sem sair de casa. Assine o Curso GUIA DO ESTUDANTE ENEM e tenha acesso a todas as provas do Enem para fazer online e mais de 180 videoaulas com professores do Poliedro, recordista de aprovação nas universidades mais concorridas do país.
