Geometria: Cônicas

AS FIGURAS SEM ARESTAS

Cônicas são curvas que nascem da intersecção de um plano com um cone

Uma casquinha de sorvete é um cone, um sólido geométrico, ou seja, uma figura que tem três dimensões – altura, largura e espessura. Qualquer corte que você faça com um plano nas paredes do cone resulta numa figura plana – uma curva plana chamada cônica. Daí vem a definição de cônicas: são curvas obtidas da intersecção de um plano com um cone.

São cônicas a circunferência, a elipse, a parábola e a hipérbole – cada uma delas com o formato definido pela inclinação em que o plano corta o cone.

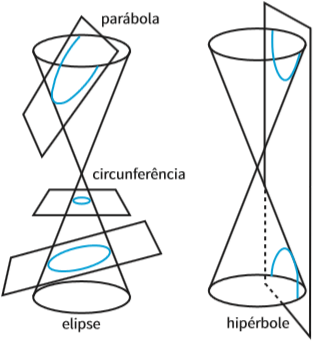Observe que a curva é alterada dependendo da inclinação do plano que corta o cone:

• Um plano perfeitamente horizontal produz uma circunferência.
• Um plano ligeiramente inclinado deforma a circunferência e cria uma elipse.
• Aumentando-se a inclinação, , a elipse não mais se fecha, e a curva se transforma numa parábola
• Um plano perfeitamente na vertical cria uma hipérbole.

Todas as cônicas podem ser representadas no plano cartesiano, por um par ordenado (x, y). A relação entre x e y é dada por uma equação. A forma mais comum é a equação reduzida, ou equação geral.

CIRCUNFERÊNCIA E CÍRCULO

A circunferência é uma curva. Não tem área.  O que tem área é o círculo – a região no interior da circunferência. A área  do círculo é dada por
A = π . r²

Circunferência 

É a curva formada por todos os pontos que estão a uma mesma distância de outro ponto – o centro da circunferência.

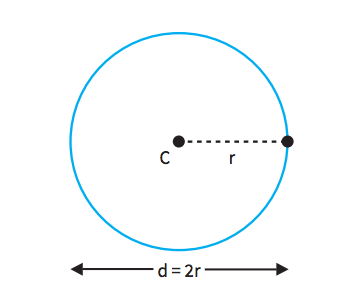
• C é o ponto que marca o centro;
• A distância de qualquer ponto da circunferência a C é o raio (r);
• Diâmetro é o dobro do raio (2r);
• O comprimento (ou perímetro) da circunferência é dado pela expressão:
  P = 2 . π . r

A letra grega π é um número irracional, que não pode ser escrito na forma de fração com numerador e denominador inteiros. Para efeito de cálculos, costumamos arredondar o valor de π para 3,14.

Equações da circunferência

Considere uma circunferência com o centro no ponto (0, 0):

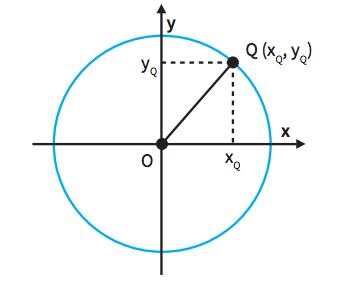
A posição de qualquer ponto Q de uma circunferência é dada por:

x_Q² + y_Q² = r²

Mas o centro da circunferência pode não coincidir com o ponto (0, 0). Considere uma circunferência que tem como centro um ponto qualquer C (a,b), e que passa pelo ponto Q (x,y). A equação reduzida para esse tipo de circunferência, cujo centro não coincide com a origem do sistema cartesiano, é

r² = (x – a)² + (y – b)²

Veja abaixo a figura:

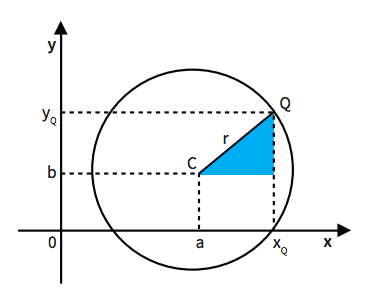
Repare que o cateto horizontal mede (x_Q – a). E o cateto vertical, (y_Q – b).

Desenvolvendo r² =  (x – a)² + (y – b)², a equação geral das circunferências fica assim:
r² = x² + y² – 2ax – 2by + a² + b²

EQUAÇÕES DA CIRCUNFERÊNCIA

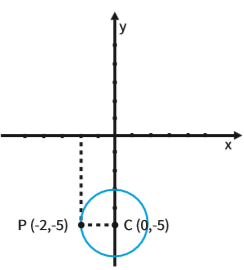
Qual o raio da circunferência com centro no ponto C (0, – 5) e que passa pelo ponto
P (-2, -5)?

Simples aplicação da equação:

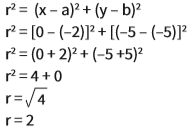
Defina as equações reduzida e geral dessa circunferência.

Para encontrar as equações de uma circunferência, basta conhecer a medida do raio e as coordenadas do centro. Sabemos que o raio é 2 e que seu centro é C (0, -5). É só aplicar esses valores nas duas equações.

Na equação geral:

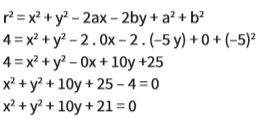
Na reduzida:

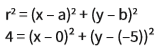
No plano cartesiano:

Inscrição e circunscrição

Circunferências inscritas em polígonos são aquelas dentro de um polígono, tocando todos seus lados. Circunferências circunscritas são aquelas que estão do lado de fora do polígono, passando por todos os seus vértices. Todos os polígonos regulares (de lados congruentes) podem ter circunferências inscritas e circunscritas. Os raios das circunferências se relacionam com as medidas dos polígonos. Veja:

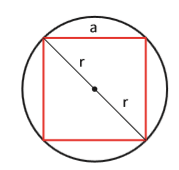
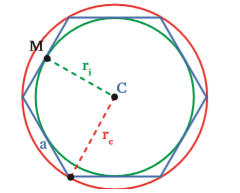
Quadrado

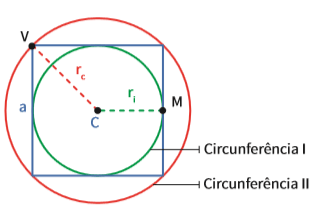
Na figura acima:

• O polígono regular é um quadrado;
• O quadrado está inscrito em uma circunferência e circunscreve outra,  de raios r_i e r_c diferentes;
• O ponto C é o centro do quadrado e das duas circunferências;
• O  ponto M é o ponto médio do lado do quadrado.

Para a circunferência inscrita:

• Ela toca o lado do quadrado no ponto médio de cada um dos lados do quadrado;
• O raio ri é a distância do centro ao ponto médio do polígono (CM). Essa distância se chama apótema (segmento de reta que une o centro a um dos lados de um polígono re- gular, sempre perpendicular a ele). O apótema sempre une o centro ao ponto médio do lado. Então, sabemos que r_i = a/2

Para a circunferência circunscrita:

• Ela toca os vértices do quadrado;
• Encontramos r_c aplicando o teorema de Pitágoras no triângulo formado por dois lados do quadrado e sua diagonal. E essa diagonal corresponde ao diâmetro da circunferência (2 . r_c). Veja:

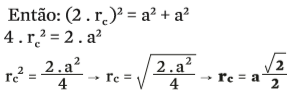
Triângulo equilátero

A circunferência inscrita toca os três lados do triângulo. A circunscrita toca seus três vértices.

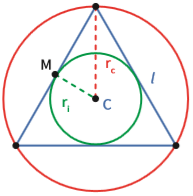
O raio da circunferência inscrita (r_i ) equivale à distância do centro C ao ponto médio do lado do triângulo. Chegamos às medidas de r_i e r_c também por Pitágoras. Não é importante que você veja a demonstração. Pode apenas guardar as equações:

Basta observar as duas equações para concluir que r_c = 2 . r_i

Hexágono regular

Também neste caso, você não precisa da demonstração. Pode apenas guardar as equações:
Para a circunferência inscrita,

Para a circunferência circunscrita,

Polígonos inscritos

Um quadrado e um triângulo equilátero estão inscritos em uma circunferência. Calcule o comprimento dos lados do triângulo equilátero, sabendo que a área do quadrado é 100 cm².
Primeiro, preste atenção no enunciado, para não se confundir: se os polígonos estão inscritos, então a circunferência está do lado de fora, circunscrevendo os polígonos. A situação descrita é esta:
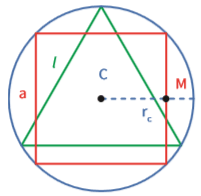O enunciado informa que a área do quadra- do é A = 100 cm².

O raio da circunferência que circunscreve um quadrado é dado por:

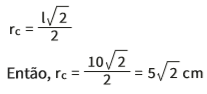
Esta circunferência circunscreve também o triângulo equilátero. A equação que relaciona o lado do triângulo com r_c é:

Elipse

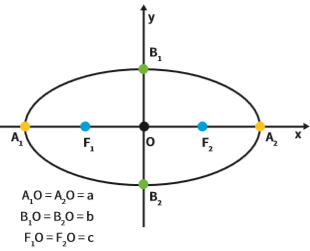
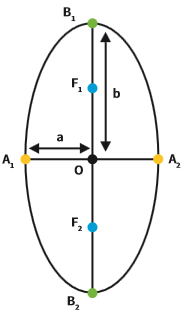
Numa definição informal, elipse é uma circunferência deformada. Veja as relações entre os elementos de uma elipse:

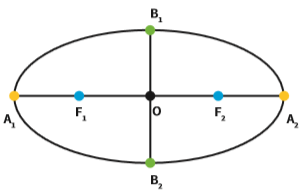
O é o centro da elipse
A₁A₂ é o eixo maior da elipse
B₁B₂ é o eixo menor da elipse
F₁ e F₂ são os focos da elipse

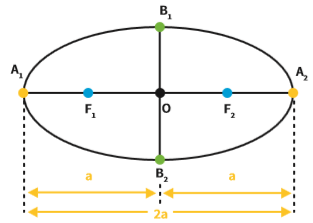
A distância entre o ponto A₁ e o centro O é sempre igual à distância do ponto A₂ ao centro O.
Se chamarmos essa distância de a, temos que A₁A₂= 2 . a

A distância entre F₁ e F₂ e o centro O é sempre igual e se chama (c).

Como F₁O = F₂O, então a distância entre F₁ e F₂ = 2 . c  (distância focal)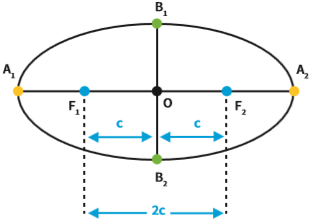

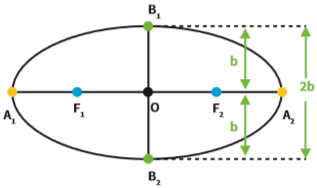
A distância entre o ponto B₁ e o centro é sempre igual à distância entre o ponto B₂ e o centro. Então, a distância entre B₁ e B₂ = 2 . b

As distâncias de um ponto qualquer da elipse a F₁ e F₂, somadas, é um valor constante.

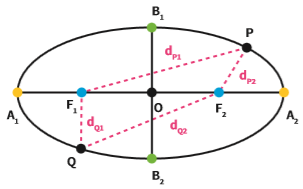
d_P1 + d_P2 = d_Q1 + d_Q2

EQUAÇÃO DA ELIPSE

Escreva a equação reduzida desta elipse.

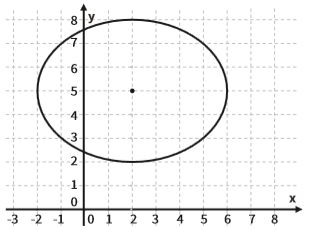
Identificamos os principais pontos da elipse.
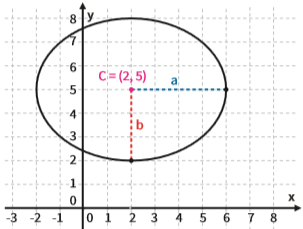Repare que C não coincide com a origem do sistema (0,0). Nesse caso, temos de considerar a diferença entre as coordenadas. Chamando as coordenadas de C de m e n, temos:

Substituindo os valores de m e n, encontramos a equação da elipse dada:

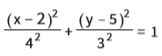
Se a elipse for vertical, a equação muda:
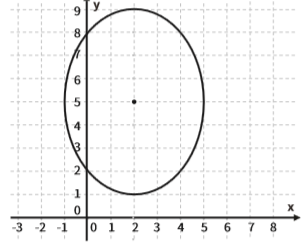Agora o eixo maior (2a) está na vertical (ou seja, sua medida é dada pelo eixo y). Então os denominadores da equação mudam de lugar:

Substituindo os valores, novamente, temos:

A elipse no plano cartesiano

Como a circunferência, uma elipse também pode ser desenhada num plano cartesiano, ou seja, sobre os eixos x e y:
Se a elipse tiver o centro na origem do sistema cartesiano – ou seja, nas coordenadas (0, 0) –, cada ponto da curva é definido pela equação:

• x e y são as coordenadas de um ponto qualquer P;
• m e n são as coordenadas do centro da elipse: O (m,n);
• a é metade do eixo maior e b, metade do eixo menor.

Essa equação descreve uma elipse cujo eixo maior está na horizontal. Para obter a elipse com eixo maior na vertical, basta trocar a e b de lugar na equação:


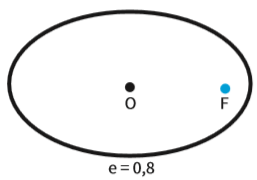
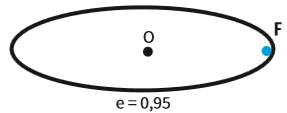
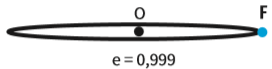
Excentricidade

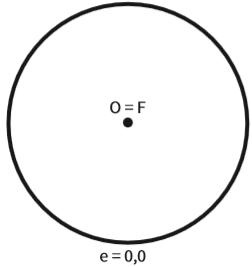
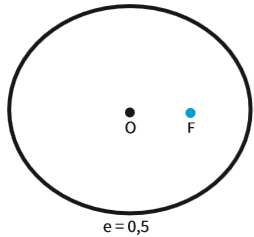
A excentricidade (e) de uma elipse é a razão entre a distância focal (2c) e o tamanho do eixo maior (2a). Em linguagem matemática:

A excentricidade é sempre um número positivo, que varia de zero a um (0 ≤ e < 1).
Isso porque c é sempre maior ou igual a zero (c ≥ 0) e sempre menor que a (c < a).

Parábola

A parábola é a curva definida por pontos para os quais a distância de uma reta diretriz é igual à distância do ponto foco (F). Veja na figura:

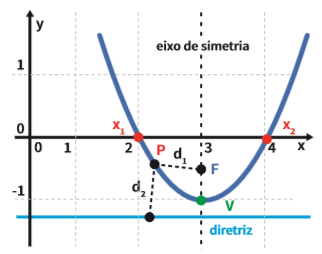
• A reta azul é a diretriz
• F é o foco da parábola
• V é o vértice
• Os valores x₁ e x₂ correspondem aos pontos em que a parábola corta o eixo x.
• P é um ponto qualquer da parábola
• As distâncias de P ao foco e de P à diretriz são iguais: d₁ = d₂.
• O eixo de simetria é a reta que passa pelo foco e pelo vértice.

As parábolas são as curvas características dos gráficos das funções do 2º grau, ou seja, das funções cuja expressão tem a forma geral y = ax² + bx + c.

Hipérbole

A figura abaixo é uma hipérbole – uma curva de dois ramos, virados para lados opostos.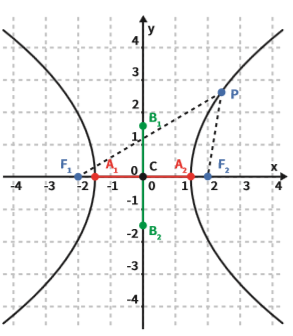
Acompanhe na figura:

•  O ponto C é o centro da hipérbole. Neste caso, C coincide com a origem do sistema cartesiano:
  C = O = (0,0);
•  F₁ e F₂ são os focos da hipérbole;
• A  distância entre F₁ e F₂ é a distância focal da hipérbole e vale 2c;
• Os pontos A₁ e A₂ são os vértices da hipérbole;
• O segmento A₁A₂ é chamado eixo real da hipérbole, e vale 2a;
• O segmento B₁B₂ é o eixo conjugado da hipérbole, e vale 2b;
• Um ponto qualquer P da hipérbole tem distâncias d₁ e d₂ dos focos F₁ e F₂. A hipérbole é formada por pontos tais que a diferença entre as distâncias d₁ e d₂ é constante, em módulo.

Quando o centro da hipérbole coincide com a origem do sistema cartesiano, a equação reduzida é:

em que x é a coordenada do ponto P no eixo x, e y, a coordenada de P no eixo y.

LUZES PARABÓLICAS. Os fogos de artifício fazem no céu curvas que lembram parábolas

ÓRBITA ELÍPTICA

A órbita de asteroides e cometas em torno do Sol é elíptica, como a dos planetas. E a velocidade desses corpos varia conforme o ponto da elipse em que se encontram. Foi o alemão Johannes Kepler quem descobriu isso, no início do século XVII. Até então, imaginava-se que as trajetórias descritas pelos planetas, asteroides e cometas tivessem a forma de circunferência.
Kepler não percebeu apenas que a órbita dos planetas é elíptica. Ele também notou que a velocidade de cada corpo celeste varia ao longo dessa trajetória.
Kepler observou que o Sol não se encontra no centro da elipse, mas em um de seus focos. Assim, os planetas estão ora mais próximos, ora mais distantes dele. E, quanto mais próximo, mais rápido o planeta viaja. Essa variação de velocidade obedece à 2ª Lei de Kepler, ou Lei das Áreas. Segundo ela, “a linha que une um planeta ao Sol atravessa áreas iguais em intervalos iguais de tempo”. Veja abaixo o que significa a Lei das Áreas, de Kepler.

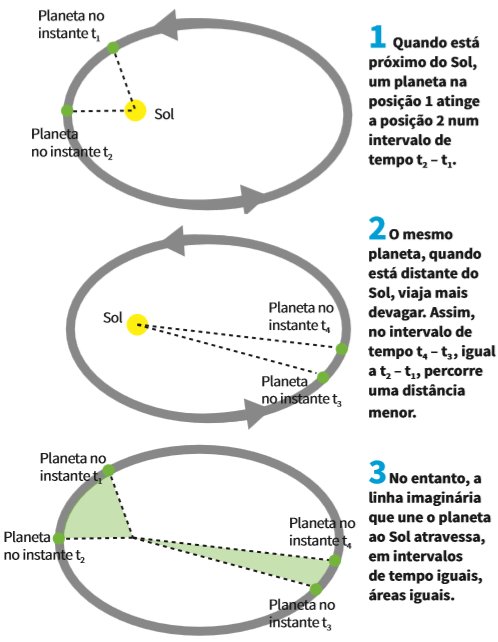
A maioria dos planetas segue órbita de excentricidade muito próxima de zero – ou seja, órbitas quase circulares. Mercúrio é o de órbita mais excêntrica, com excentricidade pouco maior que 0,2. Para a Terra, a excentricidade é de 0,017 e para Vênus, 0,007.
Mas alguns corpos que circundam o Sol têm excentricidade muito maior. O cometa Halley, que passa por aqui a cada 75 anos, descreve uma curva com excentricidade de 0,97.