Geometria: Sólidos (prismas, cones e pirâmides)

EDIFÍCIOS SÓLIDOS. Prédios modernos, como este, da Biblioteca Central de Seattle, nos Estados Unidos, exploram a combinação de figuras sólidas, como prismas
Área e volume dos principais sólidos – prismas, cones, cilindros e pirâmides
Os polígonos, você lembra, são figuras de duas dimensões, relacionadas aos lados e à altura, que permitem calcular sua área. Já as figuras tridimensionais, chamados sólidos geométricos, têm três dimensões: altura, comprimento e largura. Com essas medidas encontramos o volume de um prisma – ou seja, o espaço que ele encerra.
Tipos de sólidos
Os sólidos geométricos são divididos em duas grandes famílias:
- >> poliedros, construídos com faces que têm formato de polígonos;
- >> corpos redondos, que, se cortados, podem mostrar uma circunferência (ou um círculo) como seção.
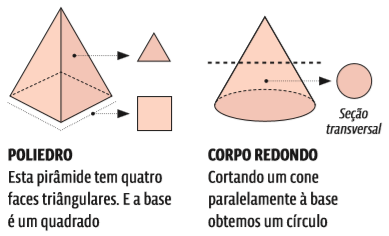
Poliedros
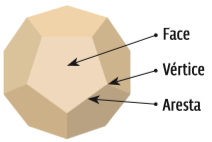
Os poliedros têm, pelo menos, quatro faces. Os polígonos que formam os lados das faces do poliedro compartilham lados entre si, formando as arestas. Os pontos onde três ou mais arestas se encontram são os vértices do poliedro.
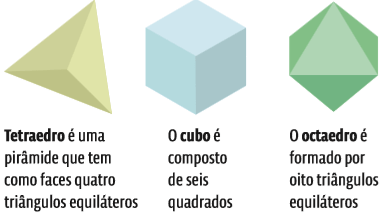
Os poliedros regulares são aqueles formados exclusivamente por polígonos regulares, ou seja, polígonos com lados iguais. Além disso, os poliedros regulares são formados por polígonos de mesmo formato e com o mesmo número de lados: só quadrados, só triângulos equiláteros ou só pentágonos regulares.
RELAÇÃO DE EULER
Todo poliedro convexo obedece à relação de Euler, que define o número de vértices (V) e faces (F) em função do número de arestas (A):
V + F = A + 2
Prismas
São poliedros em que duas das faces, de for- mato idêntico, se encontram em planos paralelos. Se os polígonos das bases forem polígonos regulares, isto é, polígonos com todos os lados de mesma medida, então o prisma é chamado de prisma regular
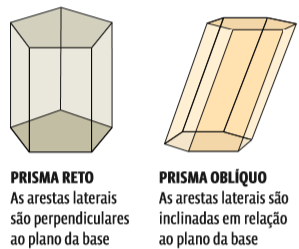
Um prisma pode ser reto ou oblíquo:

ÁREA DE PRISMA
Qual é a área total de um prisma regular, reto, de bases quadradas, com altura de 10 cm e aresta das bases de 3 cm?
Se o prisma é regular, então os lados da base são iguais: as base são quadrados.
Se o prisma é reto, então as faces laterais são perpendiculares às bases. Este é o prisma:
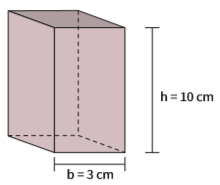
A área de um prisma regular e reto é:
Atotal = Abases + Afaces
Cada base é um quadrado.
Então, Abases = a2
Cada face é um retângulo.
Então, face = a . h
Preste atenção: você tem de levar em conta que o prisma tem duas bases e quatro faces:
Então, Atotal = 2 . 3 . 3 + 4 . 3 . 10
Atotal = 18 + 120
Atotal = 18 + 120
Os prismas também podem ser classificados conforme o tipo de polígonos das bases:
A área total de um prisma é a soma das áreas dos polígonos que formam as faces laterais e a área das bases.
Atotal = Abase + Afaces
As medidas das áreas laterais são sempre áreas de quadriláteros (polígonos de quatro lados). Se o prisma for reto, as faces laterais são retângulos.

O cubo é o prisma regular e reto mais simples que existe. Um cubo tem seis lados, todos quadrados.
Paralelepípedo reto-retângulo
Uma caixa de leite é um paralelepípedo reto-retângulo: um prisma reto de bases quadradas. É importante saber calcular a medida das diagonais desse tipo de paralelepípedo. Veja:
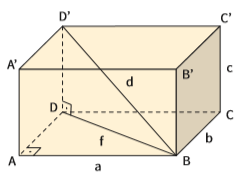
- >> A face ABCD é um retângulo;
- >> Esse retângulo tem uma diagonal f, chamada diagonal da face;
- >> Encontramos a medida de f aplicando o teorema de Pitágoras sobre as medidas dos lados a e b desse retângulo:
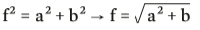
- >> O segmento que une vértices em faces de planos paralelos (d) é a diagonal do paralelepípedo. Seu comprimento, em função das dimensões a, b e c do paralelepípedo, também pode ser determinado pela aplicação do teorema de Pitágoras, agora no triângulo DBD’: d² = f² + c²
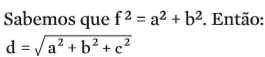
Essa é a fórmula para encontrar a diagonal de um paralelepípedo reto-retângulo de dimensões a, b e c.
Pirâmides
Pirâmide é o sólido que tem uma única base, formada de um polígono qualquer, e faces laterais na forma de triângulos com um vértice em comum. Uma pirâmide também pode ser reta ou oblíqua.
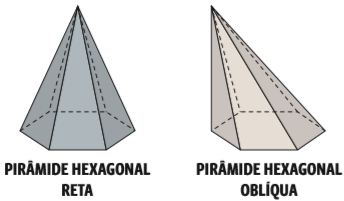
Pirâmides que têm como base um polígono regular (de lados de mesma medida) são chamadas pirâmides regulares.
Se a pirâmide for regular e reta, então os triângulos das faces laterais serão isósceles, ou equiláteros (no caso de triângulos de lados de mesma medida).
Como ocorre com qualquer sólido, o cálculo da área total de uma pirâmide é a soma das áreas da base e de cada face, no caso, cada triângulo:
Atotal = Abases + Afaces
![]()
ÁREA DE PIRAMIDE
Calcule a área total de uma pirâmide reta, de base quadrada, com 8 cm de aresta da base e 3 cm de altura. Desenhando a pirâmide:
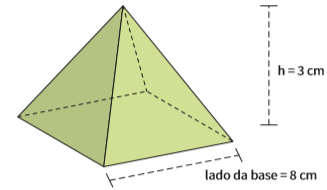
Atotal = Abase + Afaces
A base é um quadrado de 8 cm de lado. Então,
Abase = 8 . 8 = 64 cm2
As faces são quatro triângulos isósceles.
Lembrando a fórmula da área de triângulos, temos: ![]()
Sabemos que a base mede 8 cm (a mesma medida de um lado da base). Mas atenção: a altura da pirâmide não é a altura dos triângulos (que estão inclinados).
Calculamos essa altura com um truque: criamos um novo triângulo no qual um dos lados é o eixo central da pirâmide, do centro da base até o vértice (CV).
E os dois lados são os pontos CM e MV. Veja:
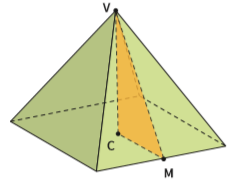
Para o triângulo CMV, sabemos que CV = hpirâmide = 3 cm
Repare que o lado CM do triângulo vale metade de um lado da base:
![]()
Repare, também, que o triângulo CMV é um triângulo retângulo. Então podemos aplicar o teorema de Pitágoras e descobrir a medida do lado VM, a hipotenusa desse triângulo:
![]()
Esta, sim, é a altura de cada triângulo das faces da pirâmide. Agora podemos calcular a área dos triângulos isósceles, pela fórmula da área de qualquer triângulo:
![]()
Como a pirâmide tem quatro triângulos nas faces, a área das faces soma 4 . 20 = 80 cm2.
Voltando ao início da resolução, a área total da superfície da pirâmide é a soma da área da base e as áreas das faces:
Atotal = Abase + Afaces • Atotal = 64 + 80 = 144 cm2
CILINDRO
Numa definição informal, cilindro é o sólido geométrico com duas bases paralelas e circulares.
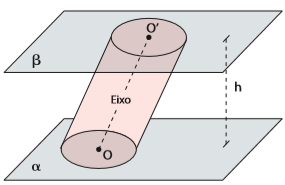
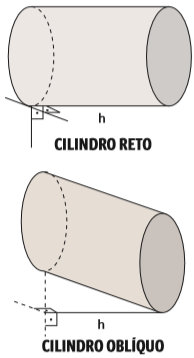
Cilindros cujas paredes laterais são perpendiculares à base são chamados cilindros retos. Caso contrário, temos um cilindro oblíquo.
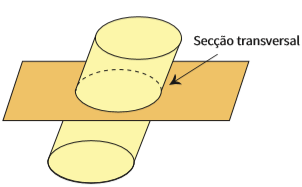
Um plano pode cortar um cilindro de diferentes maneiras. Se o corte se der por um plano paralelo às bases, a chamada seção transversal será um círculo.
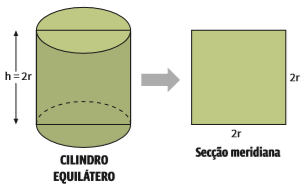
Se o plano for perpendicular às bases e passar pelo eixo do cilindro (seção meridiana), a seção é sempre um paralelogramo. Se o cilindro for reto, a seção meridiana terá a forma de um retângulo.
Como nos demais sólidos, a área total de um cilindro é a soma das áreas das bases e da lateral. Fica fácil entender como se calcula essa área com a planificação do cilindro. Planifcar signifca “abrir” o sólido em suas componentes planas. Veja o formato que um cilindro planificado tem:
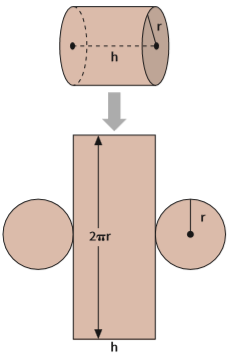
Repare que o cilindro é formado pela associação de dois círculos e um retângulo.
Sabemos que:
Atotal = Abases + Alateral
- A área de cada base é a área do círculo de raio r: A = π . r2. Como existem duas bases,
Abases = 2 . π . r2 - A área lateral é a área de um retângulo no caso de um cilindro reto (ou de um paralelogramo, no caso de um cilindro oblíquo).
Um dos lados do retângulo corresponde à altura do cilindro: h.
A medida do outro lado é exatamente a circunferência do círculo da base. Lembrando que o comprimento de um círculo é dado por C = 2 . π . r.
Então, a área lateral é dada por:
Alateral = 2 . π . r . h
Então a área total de um cilindro é:
Atotal = Abases + Alateral
Atotal = 2 . π . r2 + 2 . π . r . h
Atotal = 2 . π . r . (r + h)
Cone
Existem dois tipos de cones: o cone reto tem o eixo perpendicular à base. Quando o eixo é inclinado, temos um cone oblíquo.
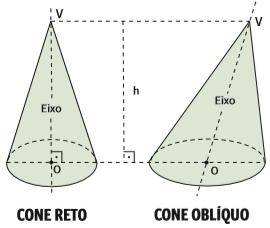
Quando um cone reto é cortado por um plano paralelo à sua base (seção transversal), a visão que se tem é a de um círculo.
A figura abaixo mostra um cone planificado.
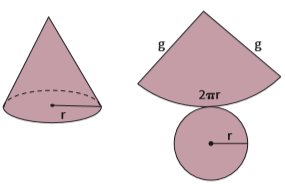
A base do cone é um círculo cuja circunferência mede 2πr. Assim, a área da base é a área de um círculo:
Abase = π . r2
Na lateral, a letra g representa um segmento de reta qualquer que liga um ponto da circunferência da base do cone a seu vértice. A superfície lateral do cone, planificada, é um setor circular – uma parte de um círculo, como um pedaço de pizza, de raio g.
O setor circular tem comprimento igual à circunferência da base (2πr). A área lateral do cone é dada por
Alateral =π.r.g
E a área total é a soma das duas áreas:
Atotal = π.r.g + π.r2 = π.r (g + r)
Volume de sólidos
O volume de prismas e cilindros é dado por:
V = Abase . h
O volume de pirâmides e cones é uma fração do volume de prismas e cilindro.
Dois sólidos têm volumes equivalentes desde que tenham mesma altura e formato e têm volumes iguais se as bases tiverem a mesma área. O volume de um cone reto é igual ao de um cone oblíquo, desde que sua altura seja a mesma e sua base tenha a mesma área. O mesmo vale entre cilindros retos e oblíquos e prismas retos e oblíquos. Fica mais fácil entender vendo a figura:
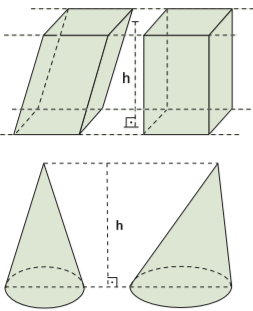
Têm volumes iguais, também, dois sólidos de diferentes formatos, desde que eles apresen- tem a mesma altura, a mesma área na base e, também, a mesma área numa seção transversal cortada à mesma altura. Este é o princípio de Cavalieri. Veja:
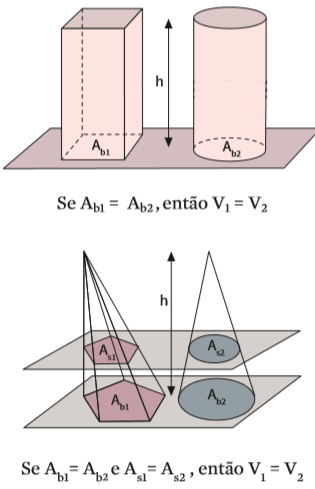

Volume da pirâmide e do cone
Uma pirâmide tem um terço do volume de um prisma com a mesma base e mesma altura. Portanto, o volume da pirâmide é dado por ![]()
A mesma relação é válida entre o cone e o cilindro:
V = 1/3 . π . r2 . h
![]()
ÁREA E VOLUME DO PRISMA
Uma caixa de 1 litro é um prisma reto, de bases quadradas e faces laterais retangulares. Sabendo que as bases têm lado igual a 5 cm, quais as dimensões de cada retângulo das faces laterais?
Este é o formato da caixa:
Se as bases são quadradas, a área de cada uma delas é a área de um quadrado:
Abase = 5 . 5
Abase = 25 cm2
O volume, sabemos, é 1 litro.
Convertendo litro para cm3: 1 L = 1000 cm3
Substituindo esses valores na fórmula para volume, temos:
V = Abase . h
1 000 = 25 . h
h = 1 000 / 25
h = 40 cm
Então, os retângulos que formam as laterais têm 40 cm de altura por 5 cm de largura.
E qual a área superficial total do prisma?
Basta somar as áreas de cada polígono das bases e das laterais:
Para a área de cada uma das bases quadradas:
A = a . a
A = 5 . 5
A = 25
São duas bases, então a área total das bases é 50 cm2.
Para a área lateral:
A = base . altura = 5 . 40 = 200 cm2
Se a base é quadrada, então só podem existir quatro retângulos.
A área total deles é: 4 . 200 = 800 cm2
Por fim, somando a área das bases e das laterais, temos:
Atotal = 50 + 800 = 850 cm2

EQUIVALÊNCIA DE VOLUMES
Dois sólidos geométricos, um prisma de base hexagonal e um cilindro, têm o mesmo volume. Além disso, ambos têm a mesma altura. Se a aresta da base do prisma mede 10 cm, qual é a medida do raio da base do cilindro?
![]()
Sabemos que dois sólidos têm volume igual desde que suas alturas e bases sejam iguais. O hexágono (base do prisma) tem área equivalente a 6 triângulos equiláteros de lados 10 cm. Sua área, portanto, é:
![]()
Se o círculo (base do cilindro) tem essa área, é fácil encontrar o tamanho do raio:
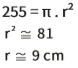

VOLUME DA PIRÂMIDE
Calcule o volume de uma pirâmide regular, de base hexagonal, com arestas da base medindo 5 cm e altura 10 cm. Primeiro, vamos calcular a área do hexágono da base. Um hexágono regular é formado por seis triângulos de lados iguais. Neste caso, o lado de cada triângulo vale 5 cm. Sabemos também que a área do triângulo equilátero em função do lado é dada por:

Se o hexágono tem seis triângulos, então,
![]()
O volume da pirâmide é um terço do volume de um prisma de mesma base e mesma altura:
![]()
Portanto,
![]()




















